
Image: Midjourney/ MomJunction Design Team
Parents looking to integrate math with fun games may consider introducing some math puzzles for kids. Playing with numbers and solving math problems not only challenges your child but also helps develop analytical skills, critical thinking, and logical thinking abilities. To motivate your child to enjoy math, ensure they have their concepts clear and they understand the basics of the subject. In this post, we bring math puzzles for children to help them develop an interest in math and clarify their basics.
Types Of Math Puzzles
Math puzzles come in various forms, each designed to challenge different aspects of mathematical thinking.
- Riddles often use clever wording to present problems requiring lateral thinking and basic arithmetic.
- Logic puzzles rely on deductive reasoning and critical thinking. Solving them involves finding patterns, relationships, or rules that govern a given set of conditions.
- Number puzzles, such as Sudoku or magic squares, engage with numerical relationships and require the solver to apply strategies involving number placement, arithmetic operations, or sequences.
Benefits of Math Puzzles
Here are some benefits of solving math puzzles:
- Math puzzles enhance problem-solving for kids to solve math problems, igniting their curiosity and interest.
- While puzzles have rules, students have the freedom to choose how to approach and solve them. This promotes independent thinking.
- Solving puzzles helps children develop problem-solving skills, enhancing their understanding of basic puzzle elements like color, letters, and characters, which can be applied to academic subjects.
- Puzzles improve the logic skills of children and boost their spatial awareness and reasoning abilities (1).
- Math puzzles create opportunities for meaningful conversations about mathematical concepts, allowing students to discuss and reinforce their understanding of previous skills.
- As group math activities for kids, solving puzzles encourages teamwork, where children can appreciate everyone’s contributions and ideas.
- Solving puzzles can give children a sense of accomplishment and enhance their confidence.
- Math tricks for kids also enhance their overall understanding of the problems, enabling them to solve logically.
Math Puzzles For Grade III (8-9 years)
1. In a meeting, there are four people. If each person shakes hands with the other, how many handshakes will happen?
Answer:
6
Explanation
Make a list of all the handshakes made by each person. There will be three handshakes per person; however, the handshakes made by A to B and B to A are the same. So, after removing such repetitions, the answer is 6 handshakes.

2. Solve the additions
Solve the below questions using the clues given
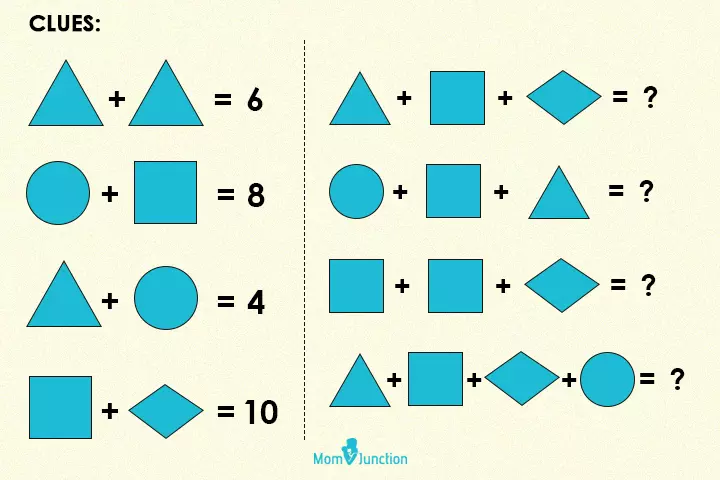
Answer:
- 3+7+3 =13
- 1+7+3 = 11
- 7+7+3 = 17
- 3+7+3+1 = 14
Explanation
According to the clues given, the sum of two triangles is 6, so each triangle’s value is 3.
The sum of a triangle and a circle is 4, since the triangle’s value is 3, the value of the circle is 1.
Similarly, the value of the square is 7, and the rhombus is 3. So, by adding the values of the shapes, we will get the above answers.
3. On one side of a highway, trees are planted adjacent to each other at an equal distance. If the distance between the first tree and the 150th tree is 660m, then what is the distance between two adjacent trees?
Answer:
4.4m
Explanation
There will be 149 gaps between 150 trees. So, the distance between two adjacent trees would require division of 660 by 149 gaps is 4.4m.
4. Find the missing numbers

13
Explanation
To solve such math puzzles, you need to identify if there is a common pattern in all four questions. Try subtraction, multiplication, and addition to find the pattern.
The sum of all the numbers in all the four questions comes up to 30, so the missing number in the last question is 13.
5. Neal, Nithin, and Noel have a set of 9 blocks each that are numbered from 1 to 9.
Each one randomly picks a set of three blocks.Neal says: The product of all the numbers with me is 63.Nithin says: The product of all the numbers with me is 48.Noel says: The sum of all the numbers with me is 16.Which numbered blocks do each of them have?Answer:
Neal: 1, 7, 9
Nithin: 2, 4, 6
Noel: 3, 5, 8
Explanation
Neal says the product of all the numbers with him is 63 and 1*7*9 is the only possible combination. Nithin might be having numbers 2, 3, 8 or 2, 4, 6, as both give the product 48. But, if Noel says the sum of the numbers with him is 16, he would have the numbers 3, 5, 8, leaving 2, 4, 6 for Nithin.
 Point to consider
Point to considerMath Puzzles For Grade IV (9-10 years)
6. When Cavin was 6 years old, his brother Mike was half his age. If Cavin is 40 years old today, how old will Mike be?
Answer:
37
Explanation
When Cavin is 6, his brother Mike’s age is 3, which is half of six. So, Cavin is three years older than Mike. Now, if Cavin is 40, then 40-3= 37 is Mike’s age.
7. What are the three whole numbers whose sum and the product are equal?
Answer:
1, 2, and 3
Explanation
1*2*3 = 6
1+2+3 = 6
8. Numbers in a triangle
Put the numbers from 1 to 9 in the blank spaces such that the sum of the numbers on each side of the triangle is the same.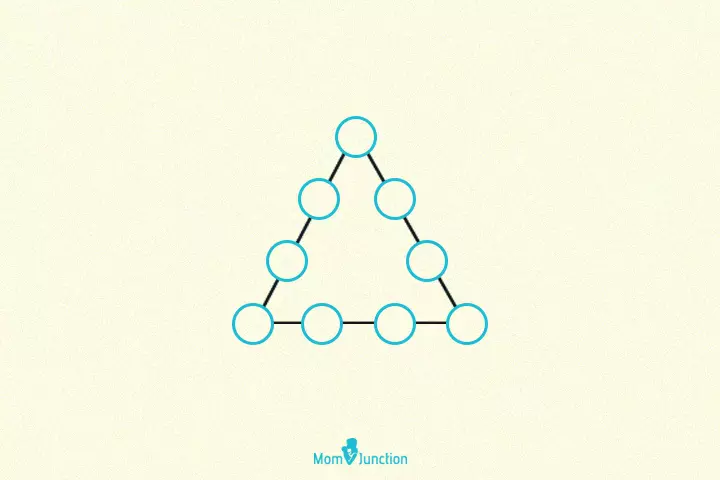
9. Linda tells Tracy, “If you gave me one of your pens, then we would have the same number of pens.” Tracy replies, “If you gave me one of your pens, then I would have twice as many as you.”
If there are a total of 12 pens, then how many pens do Linda and Tracy have each?
Answer:
Linda has 5 pens, and Tracy has 7 pens.
Explanation
Since the total number of pens is 12, let us assume Linda has 5 pens and Tracy has 7 pens.
If Linda gets one pen from Tracy, then she will have 6 pens, which are equal to Tracy’s after giving away one pen (7-1 = 6).
Tracy has 7 pens, and if Linda gives her one pen, then Tracy will have 7+1 = 8 pens, and Linda will be left with 4 pens (5-1 = 4).
10. There are 8 girls, and each girl has 8 backpacks. In each backpack, there are 8 big cats. There are 8 little cats for every big cat. How many legs are there in the bus, excluding the driver?
Answer:
18,448
Explanation
- Each girl has 8 backpacks, 8*8= 64 backpacks
- Each backpack has 8 cats, 64*8= 512 cats, one cat has four legs, 512*4= 2048 legs
- Each big cat has 8 little cats, 512*8= 4096, one cat has four legs, 4096*4= 16384 legs
- Eight girls have two legs each, 8*2= 16 legs
Total number of legs = 2048+16384+16 = 18,448
Math Puzzles For Class V (10-11 years)
11. Susan weighs half as much as Kate, and Brian weighs 3 times the weight of Susan. If the sum of their weights is 720 pounds, then how much does each of them weigh individually?
Answer:
Susan – 120 pounds
Kate – 240 pounds
Brian – 360 pounds
Explanation
Let Susan’s weight be x, then Kate’s weight will be 2x, and Brian’s will be 3x.
x + 2x + 3x = 720, then x = 720/6 = 120
So, individual weights are 120, 240, and 360 pounds.
 Point to consider
Point to consider12. Adding which four consecutive prime numbers will give you the sum of 220?
Answer:
47, 53, 59 and 61
13. When you add eight 8s, the sum should be 1000. How is this possible? (you should only use addition to solve this problem)
Answer:
888+88+8+8+8 = 1000
14. 50, 49, 47, 44, 40, 35… What comes next in the sequence?
Answer:
29
Explanation
The sequence is decreasing, so this could involve subtraction.
The difference between the successive numbers increases by a natural number. It gives us the following.
50 – 1 = 49
49 – 2 = 47
47 – 3 = 44
44 – 4 = 40
40 – 5 = 35
35 – 6 = 29
15. Apply the BODMAS rule and solve the equation.
20+30*0/1Answer:
20
Explanation: 20+30*0/1 = 20+30*0 = 20+0 = 20
16. Fill in the missing number in the last triangle

9
Explanation
You need to multiply the two corner numbers on the left hand and subtract the number in the third corner to get the number in the middle.
3*4-3 = 9
10*4-5 = 35
5*3-4 = 11
8*2-9 = 7
17. A group of soldiers was standing under the sun, facing west. The leader commanded, “Right turn! About turn! Left turn!” Which direction will they be facing now?
Answer:
East
Explanation
They turn 90° in the right turn, and they turn 180° in an about-turn, and finally, they turn 90° in a left turn, thus facing East.
18. Fill in the missing number

7
Explanation
The sequence is
85/17 = 5
76/19 =4
91/13 = 7
19. Which number should be in the place of the question mark?

12
Explanation
The two-digit numbers are the sum of each digit in the three-digit numbers.
Therefore, 5+1+6 = 12
20. Find the odd one out.
740, 185, 37, 407, 1369, 111, 78Answer:
78
Explanation
All the other numbers are divisible by 37 except 78.
Math Puzzles For Class VI (11-12 years)
21. What is the factorial of 5?
Answer:
120
Explanation
A factorial is the product of all positive integers from one to that number.
5*4*3*2*1 = 120
22. In a class of 40 students, 8 take English, 15 take French, and 6 take both languages. The students taking both the languages are not counted in the French or English taking students. How many students are not taking either French or English?
Answer:
11
Explanation
The sum of 8+15+6 is 29, which is the total number of students taking at least one of the languages. Subtract 29 from the total number of students, 40-29 = 11, it gives the number of students who are not taking any of the languages.
 Quick tip
Quick tip23. If you have 20 squares, 9 pentagons, 8 triangles, and 6 hexagons, how many total sides do you have?
Answer:
185
Explanation
20 squares = 20*4= 80
9 pentagons = 9*5= 45
8 triangles = 8*3=24
6 hexagons = 6*6= 36
80+45+24+36 = 185
24. How many crates do you need to pack 150 pairs of clothes into cases that hold 50 clothes each?
Answer:
6
Explanation
150 pairs of clothes, so 150*2 = 300 clothes
Each case can hold 50 clothes, then 300 clothes needs,
300/50 = 6 crates
25. Divide 28 by 7 and add it to 15 multiplied by 5. What is the answer?
Answer:
79
Explanation
28/7= 4
15*5= 75
75+4 = 79
26. Add ¾ of 216 to ⅗ of 75
Answer:
207
Explanation
¾ of 216 = 162
¾ of 75 = 45
162+75 = 207
27. A boy got 75 out of 90 in Hindi, 85 out of 100 in English, and 88 out of 90 in Arithmetic. In which subject his percentage of marks is the best? Also, find his overall percentage.
Answer:
Arithmetic and 88.5%
Explanation
Percentage marks in Hindi = 75/90*100 = 83.3%
Percentage marks in English = 85/100*100 = 85
Percentage marks in Arithmetic = 88/90*100 = 97.7%
He got the best percentage of marks in arithmetic.
Total marks he got = 75+85+88 = 248
Total marks = 90+100+90 = 280
Overall percentage= 248/280*100 = 88.5%
Jenna Laib says that using math place value puzzles makes her students hooked on solving them. She says, ”I scrapped my original plans for homework (and class), and instead assigned students to design their own “Inaba Place Value puzzles.” Students later worked through them when we had a spare moment in class. A few examples are shown at right. The sixth graders insisted on using more digits, and greater powers of 10. Whether in first grade, sixth, or eleventh, students seem to reach some consensus that problems are more complicated if the numbers in them are very large or very small (i).”
Illustration: Super Fun Maths Puzzles For Kids With Answers

Image: Stable Diffusion/MomJunction Design Team
Frequently Asked Questions
1. What are the benefits of math puzzles for kids?
Solving math puzzles can be a great way to bond with your children. This team-building activity can improve problem-solving skills. When children attempt to solve math puzzles or mental math equations, they learn perseverance, which encourages them to take positive risks later in life.
2. What are the math puzzles called?
Sudoku is the most popular math puzzle, followed by the Kakuro puzzle.
3. Do math puzzles help with kids’ brain development?
Yes. Math puzzles and their calculations act as brainteasers and are a great brain exercise. Practicing math regularly aids in brain workouts that make children smarter and is also effective in stress reduction. While solving math puzzles, the brain is forced to gain concentration to focus solely on a single task and come up with a strategy for reasoning that relieves stress caused by scattered focus and multitasking.
4. How can I incorporate math puzzles into my child’s routine?
Introduce a daily math puzzle as a warm-up exercise before homework, setting a positive tone for the study session. You can also dedicate a day to math-related board games or online puzzle challenges. Additionally, you can subscribe to a math puzzle app or website that offers daily challenges, encouraging your child to solve them independently or as a family.
Math puzzles for kids work like magic when it comes to improving their mathematical skills. Solving such puzzles is fun and encourages them to think out of the box and use memory, creativity, and imagination to find a solution. If you present the problems in the form of math riddles for kids or puzzles, they would love to practice math and develop their skills over time. These puzzles are interesting and keep kids engrossed deeply in them for a long time.
Key Pointers
- Solving math puzzles can spark curiosity in children and hone their analytical and critical thinking abilities.
- When children solve these puzzles independently, it encourages them to think independently and make their decisions.
- Math puzzles enable children to apply their logic and reasoning skills, which can help them understand complex concepts more quickly.
- Each time a child successfully solves a problem, it boosts their confidence and motivates them to take on more challenges.
- Puzzles can help children learn maths in a more fun and engaging manner.
Are you looking to boost your brain power by 80%? Check out this video to learn 10 fun math games that will help you do just that!
Personal Experience: Source
MomJunction articles include first-hand experiences to provide you with better insights through real-life narratives. Here are the sources of personal accounts referenced in this article.
i. Inaba’s place value puzzles: Making connections and asking “What If”https://jennalaib.com/2017/02/21/inabas-place-value-puzzles-making-connections-and-asking-what-if/
References
- Puzzle Play: An Easy Way to Boost Early Spatial and Math Learning
https://dreme.stanford.edu/news/puzzle-play-an-easy-way-to-boost-early-spatial-and-math-learning/
Community Experiences
Join the conversation and become a part of our nurturing community! Share your stories, experiences, and insights to connect with fellow parents.
Read full bio of Elisa Yi
Read full bio of Nisha Bharatan
Read full bio of Harshita Makvana
Read full bio of Trisha Chakraborty

















